Entropy Extraction and Error Correction of Images for Cryptographic Applications
Currently prevailing techniques in cryptography and computer security rest on the tacit assumption that all communication partners can safely and permanently store a secret key (i.e., a secret digital number) that remains unknown to adversaries. Unfortunately, various strategies for extracting such keys from electronic systems, such as invasive, side-channel, or malware attacks, have been developed over the years.
The novel, innovative primitive of Strong Physical Unclonable Functions (Strong PUFs) offers a seminal alternative in this situation: It empowers communicants to identify themselves to others without permanently storing digital keys in their systems. This enables certain forms of advanced, “keyfree” security. The currently most promising implementation of Strong PUFs are complex optical systems, in which laser light is scattered multiple times, creating a highly complex interference pattern as output [1]. The situation is shown schematically in Figure I.
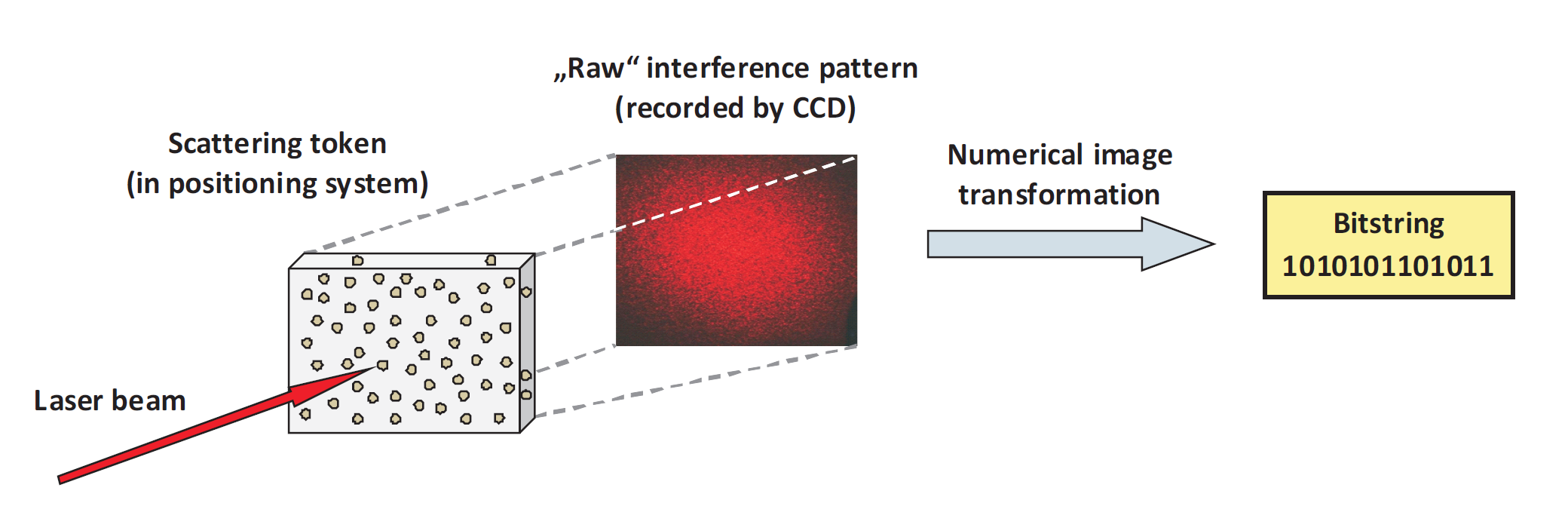
Figure I: Basic schematics of an optical Strong PUF [1]: A laser beam hits a randomly structured scattering token. The laser light is scattered multiple times and creates a highly complex interference pattern, which must be postprocessed, producing a stable bitstring. This bitstring should be stable upon multiple measurements (in opposition to the interference pattern and its small fluctuations). The bitstring should also have maximal entropy (again in opposition to the interference pattern and its grain-like structure). Both tasks can be accomplished in combination by choosing and applying the right image transformation.
The general goal of this project is to identify, optimize and apply various numerical image processing algorithms. They shall extract or “distil” a short numeric bitstring (few thousand bits) from a complex optical image (with millions of bits measured by a CCD camera), as shown in Figure I. An optimal image transformation algorithm should meet the following requirements:
- Stabilize the extracted bitstring, information content of the response image,
- Optimize the extracted entropy and the “randomness” of this bitstring.
Prerequesites:
The candidate should have a strong background in mathematics or computer science. You should have basic knowledge of mathematical transforms, image processing and programming. You will work in an international research team with partners from the European Laboratory for Nonlinear Spectroscopy in Italy, the Ludwig Maximilian University of Munich, and the University of Passau.
Overview of tasks:
- Become familiar with the B-spline wavelet transform.
- Apply the B-spline wavelet transform to the speckle pattern images.
- Optimize the parameters of the B-spline wavelet transform and the considered wavelet bands such that the maximal information is extracted from the speckle images, and such that errors become minimal while maximizing the entropy of the binary cryptographic key.
- Compare the performance of the B-spline wavelet transform with other multiscale transforms such as the Gabor transforms, Daubechies wavelets and with morphological fiters.
Basis Literature:
- Pappu, R., Recht, B., Taylor, J. and Gershenfeld, N., “Physical one-way functions.”, Science 2002, 297, 2026.
- Rührmair, U., Hilgers, C., Urban, S., Weiershäuser, A., Dinter, E., Forster, B. and Jirauschek, C., “Optical pufs reloaded.”, Eprint. Iacr. Org. 2013
Organisatorisches
Aufgabensteller:
Prof. Dr. D. Kranzlmüller
Dauer der Arbeit:
- Masterarbeiten: 6 Monate
Anzahl Bearbeiter: 1
Betreuer:
- Tobias Guggemos
- Sophia Grundner-Culemann
- Pascal Jungblut (Experte: System Programming)
- Prof. Dr. Brigitte Forster (Experte: Image Transformation)
- Prof. Dr. Dr. Ulrich Rührmair (Experte: Physical Unclonable Functions)
Diese Seite wurde 2625 mal aufgerufen.